
Subject: Class 11 Physics Online Coaching For Neet Exam
Phone: +91-9868233590
Class 11 Physics Online Coaching For Neet Exam
System Of Particles and Rotational Motion Class 11 Physics Notes
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
CENTRE OF MASS
Centre of mass for a system of particles is defined as that point where the entire mass of the system is imagined to be concentrated.
If  ......... be the position vectors of masses m1, m2, m3 ....... respectively from the origin O,
......... be the position vectors of masses m1, m2, m3 ....... respectively from the origin O,
then the centre of mass of the system is
where M is the total mass of the system of particles. The product of mass of the particles and its position vector w.r.t. the reference point is called moment of mass.
i.e., moment of mass 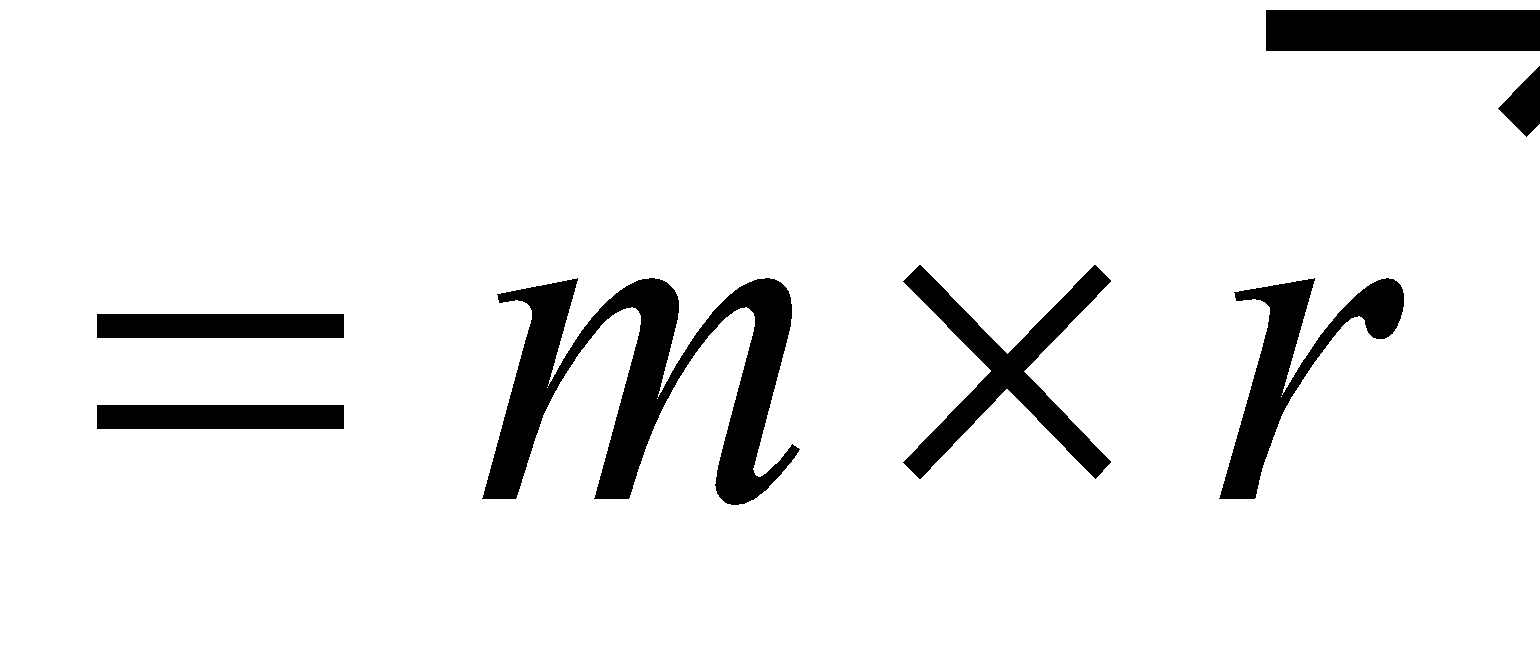
MOTION OF CENTRE OF MASS
The motion of the centre of mass is governed by the equation
Momentum conservation of a system of particles :
In the absence of external forces, the velocity of the centre of mass remains constant.
We have, MAcm = Fext
If Fext = 0
∴ vcm = constant.
Hence, momentum (Mvcm = constant) of the centre of mass system is conserved.
RIGID BODIES
If a body does not undergo any change in shape by the action of a force, it is said to be rigid.
If such body undergoes some displacement, every particle in it undergoes the same displacement. No real body can be perfectly rigid.
ROTATORY MOTION
A body rotating about a fixed axis then every particle of the body moves in a circle and the centres of all these circles lie on axis of rotation. The motion of the body is said to possess rotational motion.
KEEP IN MEMORY
- The centre of mass of a system of two identical particles lies in between them on the line joining the particles.
- If m1 = m2
so, for particles of equal masses the centre of mass is located at the mean position vector of the particles.
- The position of centre of mass remains unchanged in pure rotatory motion. But it changes with time in translatory motion or rolling motion.
- The position of centre of mass of a body is independent of the choice of coordinate system.
- If we take the centre of mass at the origin, then the sum of the moments of the masses at of the system about the origin is zero.
- In pure rotatory motion, the axis of rotation passes through the centre of mass.
- If external force is zero then the velocity of the centre of mass of a body remains constant.
- The centre of mass and centre of gravity of a body coincide, if the value of g is same throughout the dimension of the body.
- In kinematics and dynamics, whole of the mass of a body can be assumed to be concentrated at the centre of mass.
- The location of the centre of mass depends on the shape and nature of distribution of mass of the body.
- The position of centre of mass of continuous bodies can be found using integration as
where, x, y and z are the coordinates of small mass dm and M is the total mass of the system.
- The C.M. of a uniform rod of length L is at its middle point.
- Centre of mass of a uniform semicircular wire is at
, where R is the radius of the semicircular wire. It does not depend on mass.
- For symmetrical bodies of uniform mass distribution, the C. M. lies at the geometrical centre
ANGULAR VELOCITY AND ANGULAR ACCELERATION
The angular velocity is defined as the angle covered by the radius vector per unit time. It is denoted by ω.
Average angular velocity 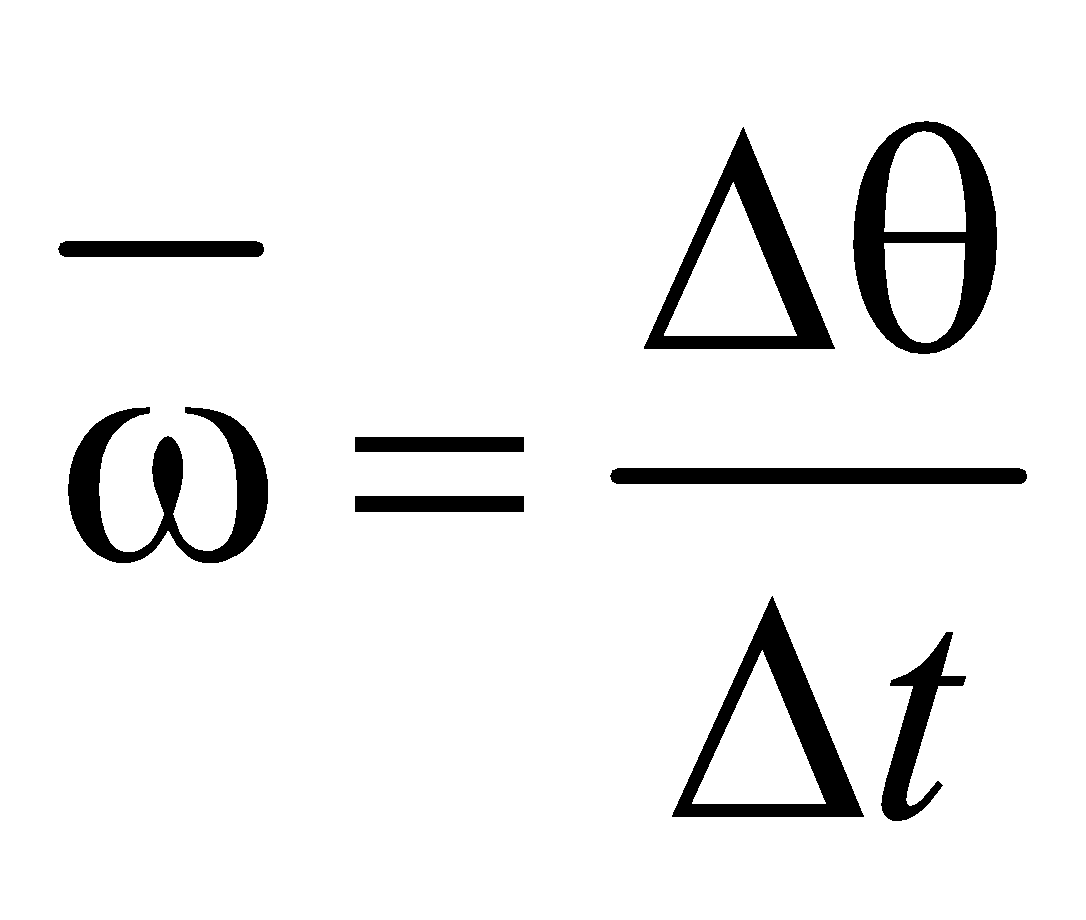
The unit of angular velocity is rad/sec.
The instantaneous angular velocity ω (similar to instantaneous linear velocity) is defined as
The angular acceleration is the rate of change of angular velocity. It is denoted by α.
The average angular acceleration αavg.of a rotating body is
In analogy to linear acceleration , the instantaneous angular acceleration is defined as
, the instantaneous angular acceleration is defined as
The unit of angular acceleration is rad/sec2.
Relationship between angular velocity and linear velocity:
where θ is the angle between ω & r.
MOMENT OF INERTIA AND RADIUS OF GYRATION
A rigid body having constituent particles of masses m1, m2, ....mn and r1, r2 ... rn be their respective distances from the axis of rotation then moment of inertia is given by,
I = m1 r12 + m2 r22 + ... + mn rn2 = 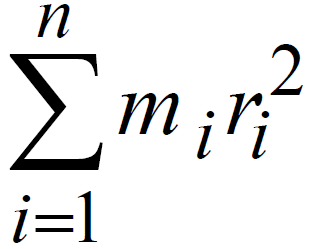
The moment of inertia of continuous mass distribution is given by
where r is the perpendicular distance of the small mass dm from the axis of rotation.
Its SI unit is kgm2. It is a tensor.
RADIUS OF GYRATION
The radius of gyration of a body about its axis of rotation may be defined as the distance from the axis of rotation at which, if the entire mass of the body were concentrated, its moment of inertia about the given axis would be same as with its actual distribution of mass.
Radius of gyration k is given by,
I = MK2
or 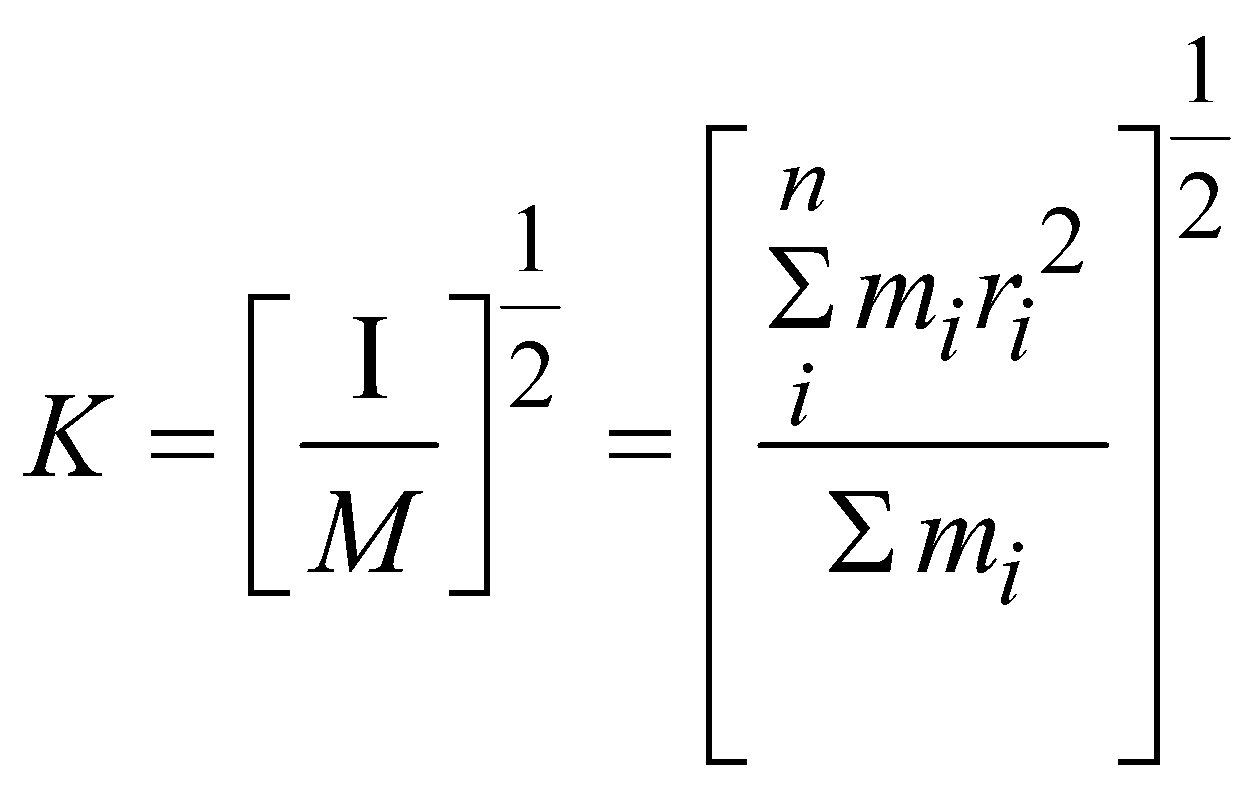
where, M = Σmi
Also, 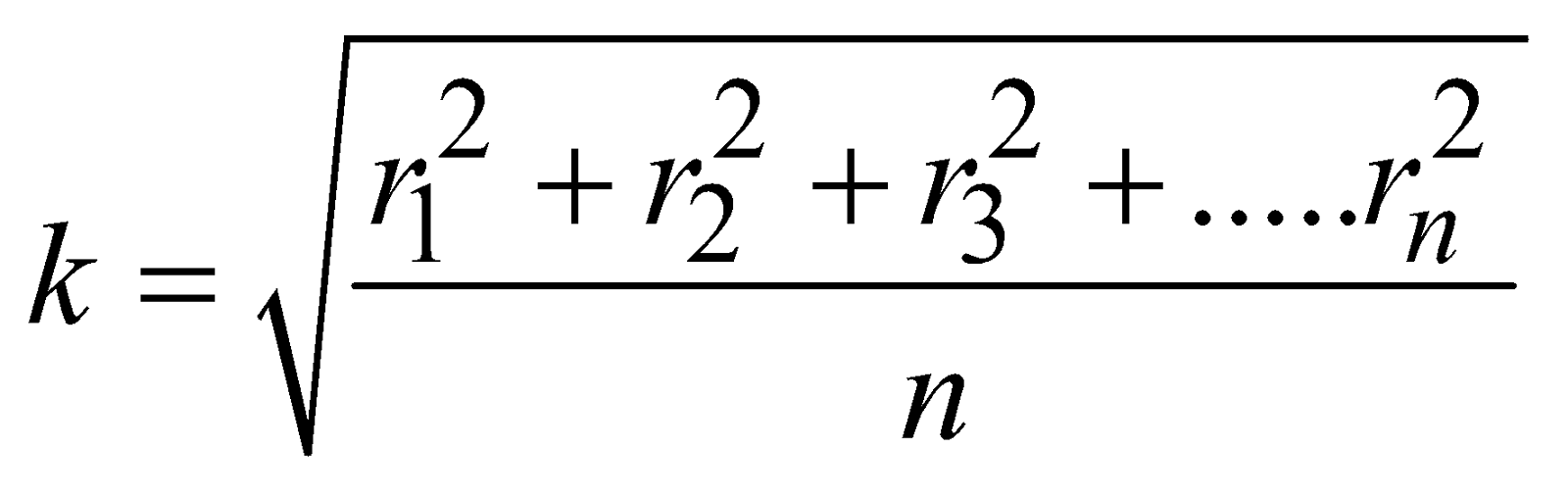
Therefore, radius of gyration (k) equals the root mean square of the distances of particles from the axis of rotation.
GENERAL THEOREMS ON MOMENT OF INERTIA
THEOREM OF PERPENDICULAR AXIS
According to this theorem “the moment of inertia of a plane lamina (a plane lamina is a 2-dimensional body. Its third dimension is so small that it can be neglected.) about an axis, perpendicular to the plane of lamina is equal to the sum of the moment of inertia of the lamina about two axes perpendicular to each other, in its own plane and intersecting each other at the point, where the perpendicular axes passes through it.”
If Ix and Iy be the moment of inertia of a plane lamina (or 2D rigid body) about the perpendicular axis OX and OY respectively, which lie in plane of lamina and intersect each other at O, then moment of inertia (Iz) about an axis passing through (OZ) and perpendicular to its plane is given by
Ix + Iy = Iz
Let us consider a particle of mass m at point P distance r from origin O, where 
so Ix + Iy = Σmy2 + Σmx2 = Σmr2
i.e., Iz = Ix + Iy
THEOREM OF PARALLEL AXES
(Derived by Steiner) This theorem is true for both plane laminar body and thin 3D body. It states that “the moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of mass plus the product of the mass of the body and the square of the distance between two axes.”
Let AB be the axis in plane of paper about which, the moment of inertia (I) of plane lamina is to be determined and PQ an axis parallel to AB, passing through centre of mass O of lamina is at a distance ‘r’ from AB.
Consider a mass element m of lamina at point P distant x from PQ. Now the moment of inertia of the element about AB = m (x + r)2 so moment of inertia of whole lamina about AB is
I = Σm(x+r)2 = Σmx2 + Σmr2 +2 Σmxr
Where first term on R.H.S is Σ mx2 = Ic.m. moment of inertia of lamina about PQ through its centre of mass, second term on R.H.S. is Σmr2 = r2Σm = Mr2, M is whole mass of lamina, third term on R.H.S is (Σmx) r = 0, because Σmx is equal to moments of all particles of lamina about an axis PQ, passing through its centre of mass. Hence
I = Ic.m. + M.r2
i.e., the moment of inertia of lamina about AB = its moment of inertia about a parallel axis PQ passing through its centre of mass + mass of lamina×(distance between two axes)2
MOMENT OF INERTIA AND RADIUS OF GYRATION OF DIFFERENT OBJECTS
TORQUE, ANGULAR MOMENTUM AND ANGULAR IMPULSE
TORQUE
The moment of force is called torque. It is defined as the product of force and the perpendicular distance of the force from the axis of rotation.
i.e., 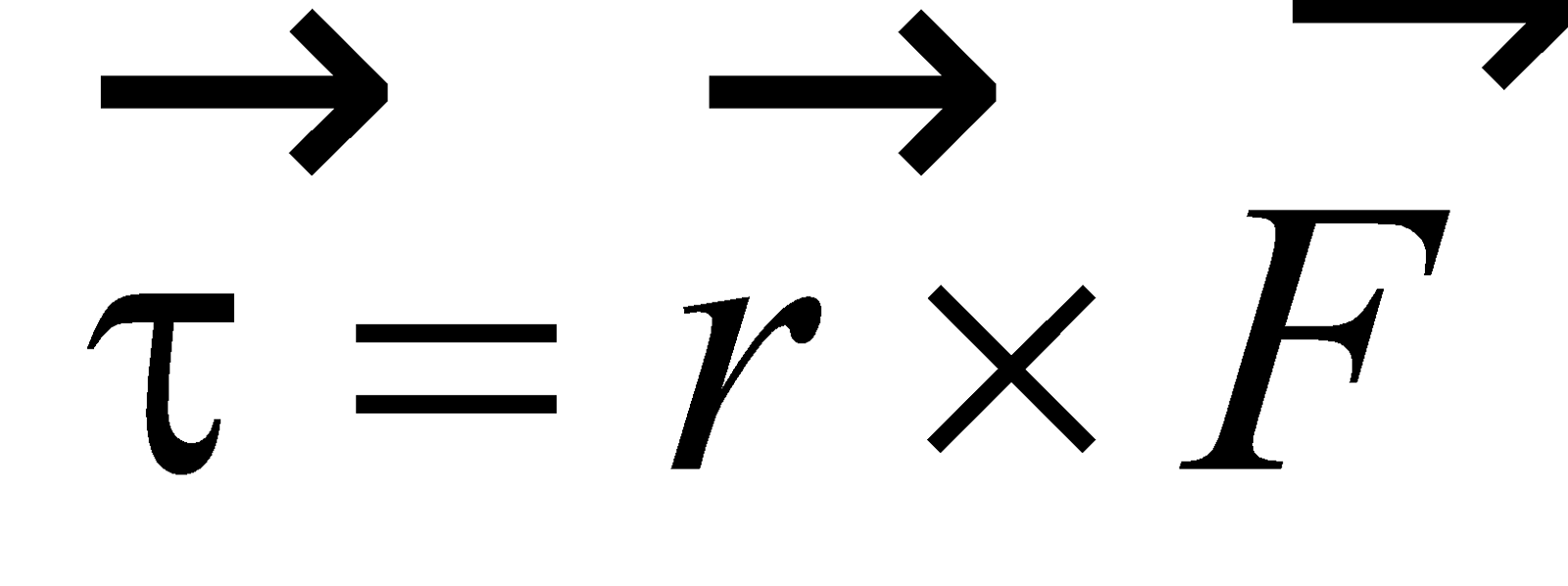
or, 
where θ is the angle between and .
Its S.I. unit is (N-m).
The dimensions of torque [ML2T–2] are the same as that of energy but it is not energy.
Note : If the line of action of a force passes through axis of rotation then no torque will be formed.
ANGULAR MOMENTUM
The angular momentum of a particle about an arbitrary point 'O' is the moment of linear momentum taken about that point.
It is given as 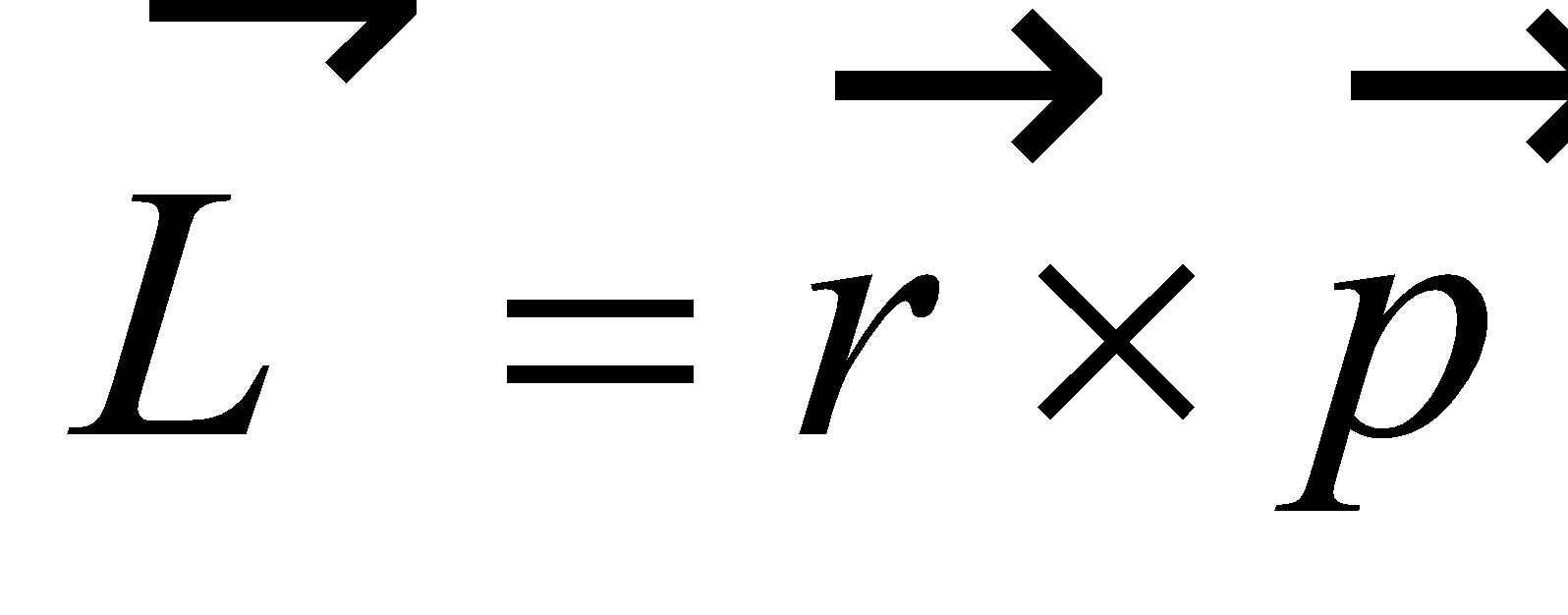
or, 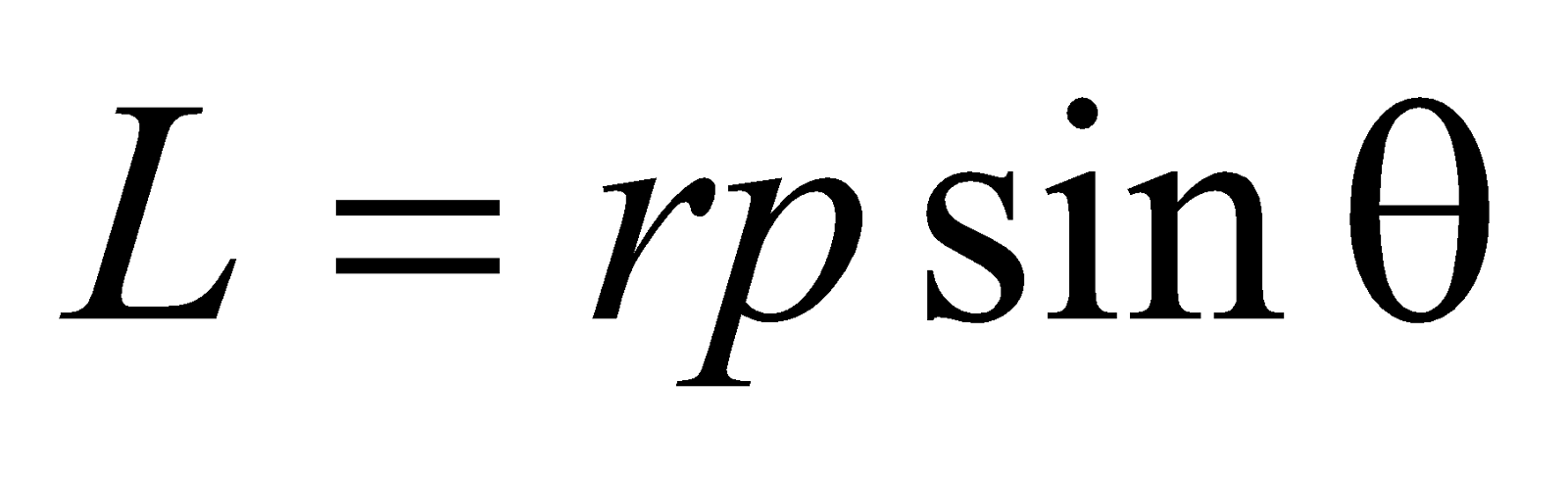
where θ is the angle between  and
and  .
.
ANGULAR IMPULSE
CONSERVATION OF ANGULAR MOMENTUM
From equation . 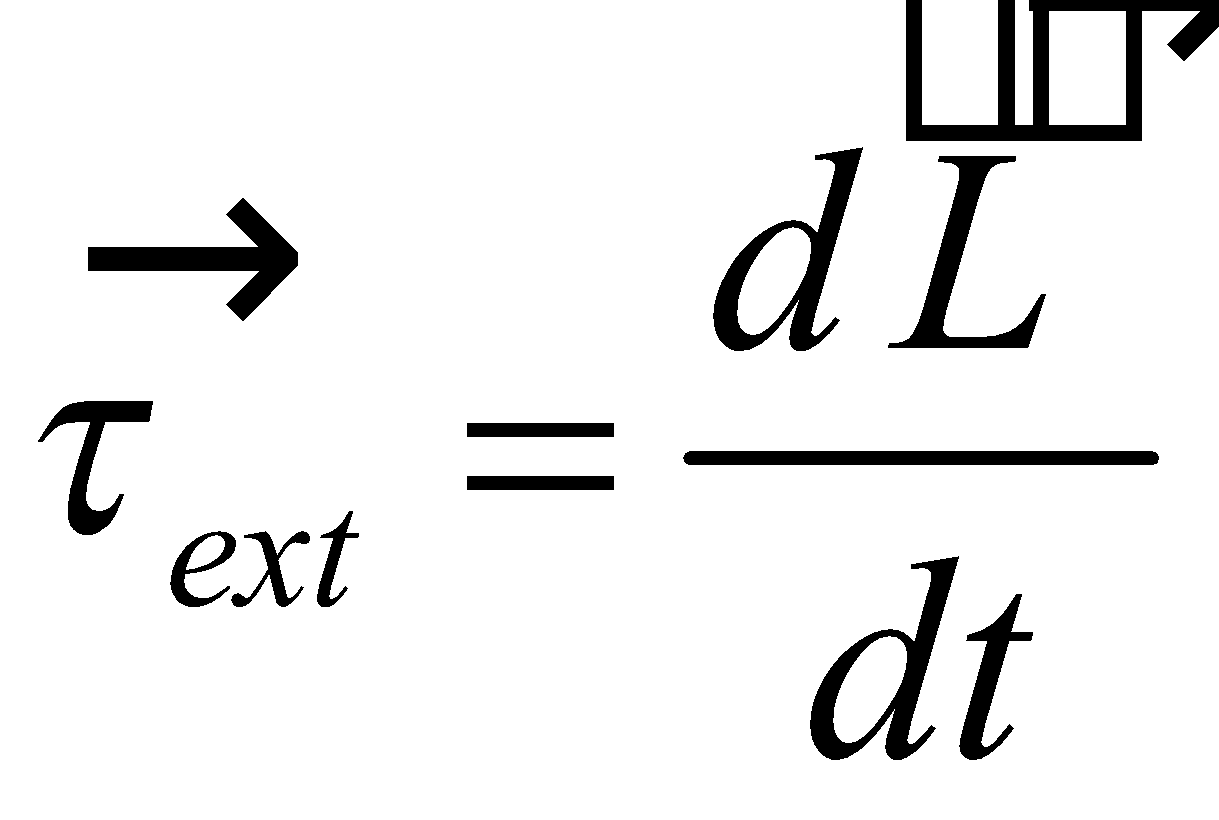
If  ...(i)
...(i)
This is called law of conservation of angular momentum.
According to this “if resultant external torque  acting on the system is zero then total angular momentum of the system is constant.”
acting on the system is zero then total angular momentum of the system is constant.”
The magnitude of angular momentum for a system is given by
Where Ii is the moment of inertia of the ith particle of that system and I is total moment of inertia of the system
or  ...(iii)
...(iii)
So if a system undergoes a redistribution of its mass, then its moment of inertia changes but since no external torque is applied on the system so total angular momentum is constant before and after the distribution of mass, even if moment of inertia of the system is changed.
or, I1ω1 = I2ω2 ...(v)
where L initial denote the state previous to the redistribution of mass and final denote the state after the redistribution of mass in that system.
A comparison of useful relations in rotational and translational or linear motion :
Rotational motion about a fixed axis
|
Linear motion
|
Angular velocity
|
Linear velocity
|
Angular acceleration
|
Linear acceleration
|
Resultant torque τ = Iα
|
Resultant force F = ma
|
Equations of rotational motion
|
Equations of linear motion
where (s = x – x0) |
Work
|
Work
|
Kinetic energy Ek = ½ Iω2
|
Kinetic energy Ek=½ mv2
|
Power P = τω
|
Power P =
|
Angular momentum L =
|
Linear momentum p = mv
|
Torque
|
Force
|
WORK ENERGY THEOREM IN ROTATIONAL MOTION
According to this theorem “the work done by external forces in rotating a rigid body about a fixed axis is equal to the change in rotational kinetic energy of the body.”
Since, we can express the torque as
τ = Iα
but τdθ = dW
⇒ τdθ = dW = Iωdω
By integrating the above expression, we get total work done by all external force on the body, which is written as
where the angular velocity of the body changes from ω1 to ω2 as the angular displacement changes from θ1 to θ2 due to external force  on the body.
on the body.
ROTATIONAL KINETIC ENERGY
Let us consider a rigid body (collection of small particles) of high symmetry which is purely rotating about z-axis with an angular velocity ω. Each particle has some energy, determined by mi and vi. The kinetic energy of mi particle is
Fig. The total kinetic energy of the body is ½Iω2.
Now we know that in rigid body every particle moves with same angular velocity, the individual linear velocities depends on the distance ri from the axis of rotation according to the expression (vi = riω). Hence the total kinetic energy of rotating rigid body is equal to the sum of kinetic energies of individual particles.
where  is moment of inertia of the rigid body.
is moment of inertia of the rigid body.
Now consider a rigid body which is rolling without slipping. In this case it possesses simultaneous translatory motion and rotatory motion and the total kinetic energy of the rigid body
K.ETotal = rotation K.E. + translational K.E. of C.M.
Ek =  ... (iii)
... (iii)
Ek =  ... (iv)
... (iv)
where,
vcm = linear velocity of the centre of mass of the rigid body
K = radius of gyration 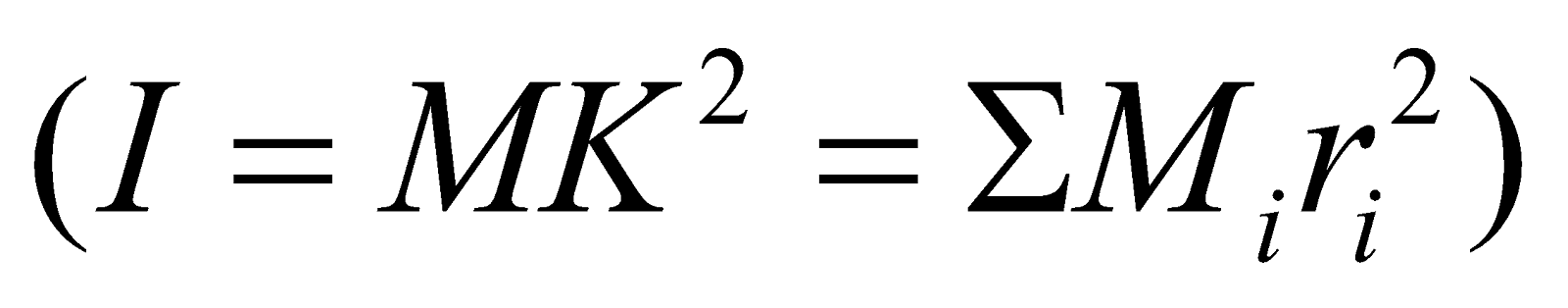
r = radius of moving rigid body
I = moment of inertia of the rigid body about centre of mass
½ Iω2 = rotational kinetic energy about the centre of mass.
Hence it is clear from the expression that total kinetic energy of rolling body is equal to the sum of rotational kinetic energy about centre of mass (C.M.) and translational kinetic energy of the centre of mass of body.
BODY ROLLING WITHOUT SLIPPING ON AN INCLINED PLANE
When a body performed translatory as well as rotatory motion then we can say that the body is in rolling motion.
Acceleration for body rolling down an inclined plane without slipping
Let M is the mass of the body, R is its radius and I is the moment of inertia about the centre of mass and K is the radius of gyration.
Force equation,  ...(1)
...(1)
Torque equation, 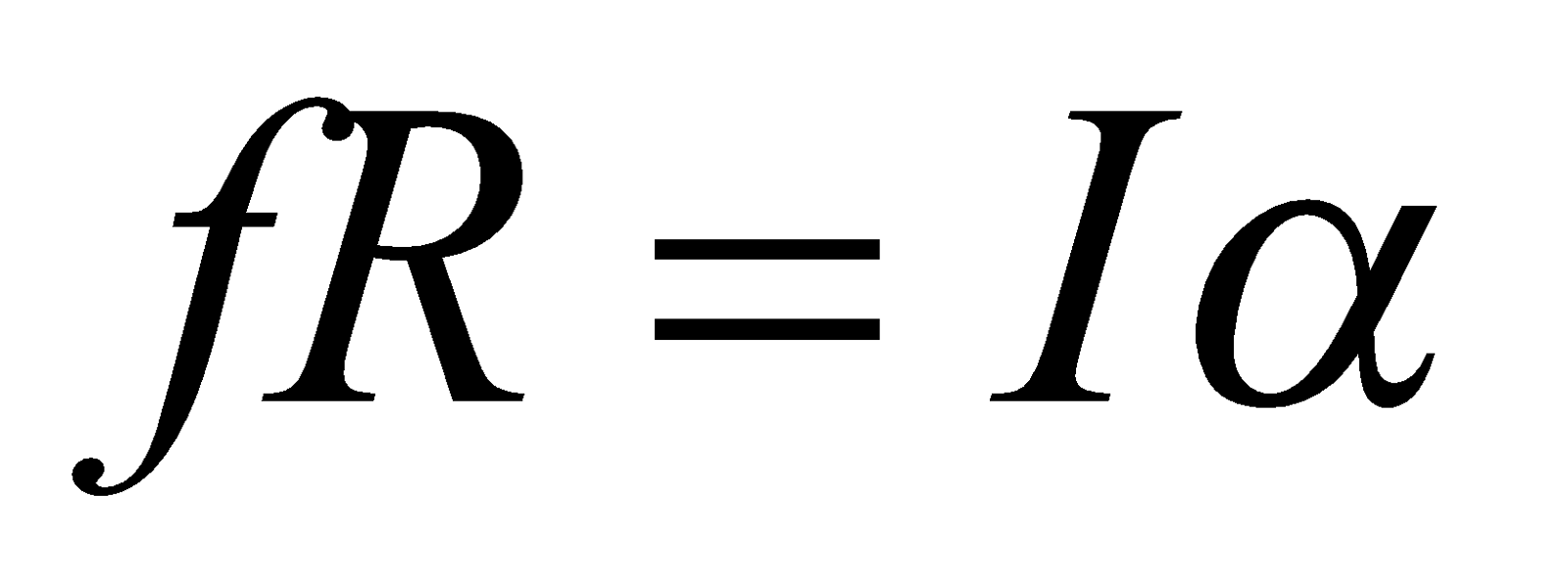 ...(2)
...(2)
Also, 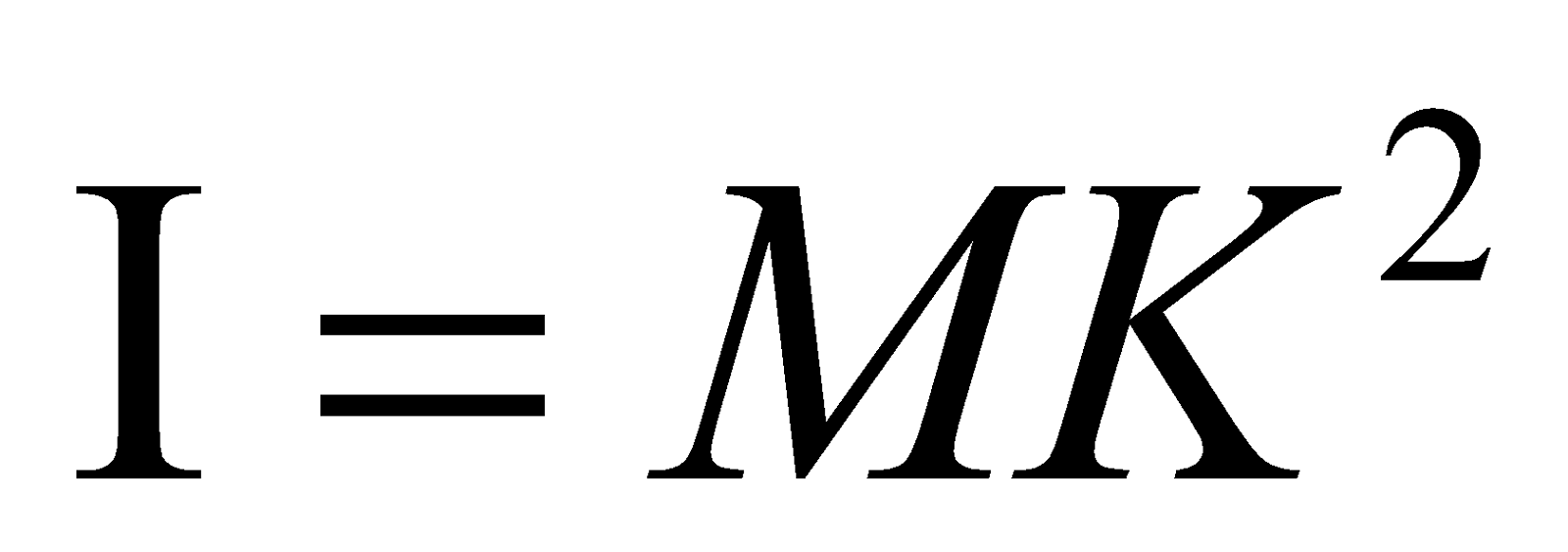 ...(3)
...(3)
Adding, eqn. (1) & (4)
Now assume in fig. that a body (which has high symmetry such as cylinder, sphere etc.) is rolling down an incline plane without slipping. This is possible only if friction is present between object and incline plane, because it provides net torque to the body for rotating about the centre of mass (since the line of action of the other forces such as mg and R pass through the centre of mass of rigid body, hence they do not produce torque in a body about the centre of mass).
A round object rolling down an incline, mechanical energy is conserved if no slipping occurs.
But mechanical energy of the body remains constant despite of friction because the contact point is at rest relative to the surface at any instant.
For pure rolling motion vc = rω
so 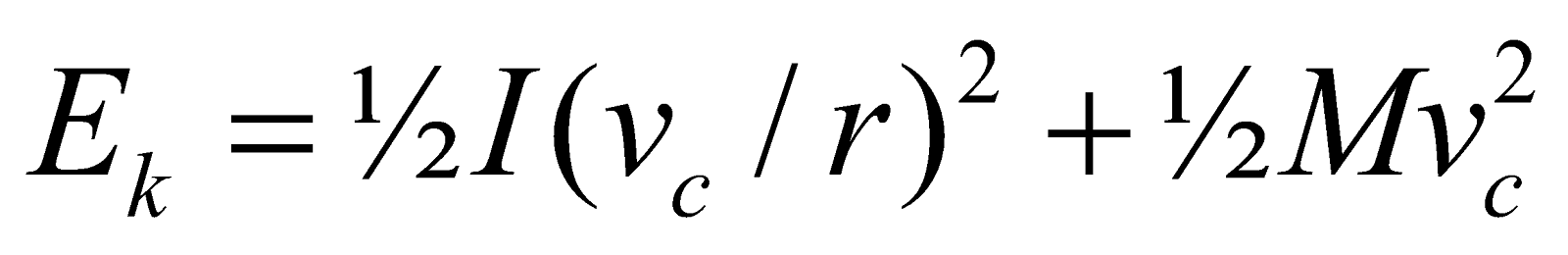
As body rolls down an incline, it loses potential energy Mgh (h is the height of incline). Since body starts from rest at top, hence its total kinetic energy at bottom given by eqn.(i) must be equal to Mgh at top i.e.,
since h =x sin θ, where x is length of incline and Ic =MK2
(K is radius of gyration), then
(K is radius of gyration), then
For rolling down an inclined plane without slipping, the essential condition is :
where Icm is moment of inertia of the body about its C.M.
DIFFERENT TYPES OF MOTION
PURE TRANSLATIONAL MOTION
In this case the velocities at all three points :
- top most point P
- C.M.
- contact point O are same
PURE ROTATIONAL MOTION
In this case the velocity of
- top most point P is Rω
- C.M. is zero
- contact point O is – Rω
ROLLING MOTION - COMBINATION OF TRANSLATORY AND ROTATORY MOTION
- In pure rolling motion, the contact point O remains at rest.
- In pure rolling, the velocity of top most point is,
V = Vcm + ωR = 2Vcm
- In rolling without slipping Vcm = ωR.
KEEP IN MEMORY
- The axis of the rolling body is parallel to the plane on which the body rolls in case of sphere, disc, ring.
- Let (Ek)r = rotational kinetic energy
(Ek)t = translational kinetic energy
For solid sphere, (Ek)r = 40% of (Ek)t
For shell (Ek)r = 66% of (Ek)t
For disc, (Ek)r = 50% of (Ek)t
For ring, (Ek)r = (Ek)t
- Translational kinetic energy is same for rolling bodies having same M, R and ω irrespective of their shape.
- Total energy is minimum for solid sphere and maximum for ring having same mass and radius.
- Rotational kinetic energy is maximum for ring and minimum for solid sphere of same mass and radius.
- (i)The acceleration down the inclined plane for different shapes of bodies of same mass and radius are as follows : Sphere > disc > shell > ring
(ii) The velocity down the plane is related as follows: Sphere > disc > shell > ring
(iii) The time taken to reach the bottom of the inclined plane is related as follows : Ring > shell > disc > sphere.
This is because
For ring 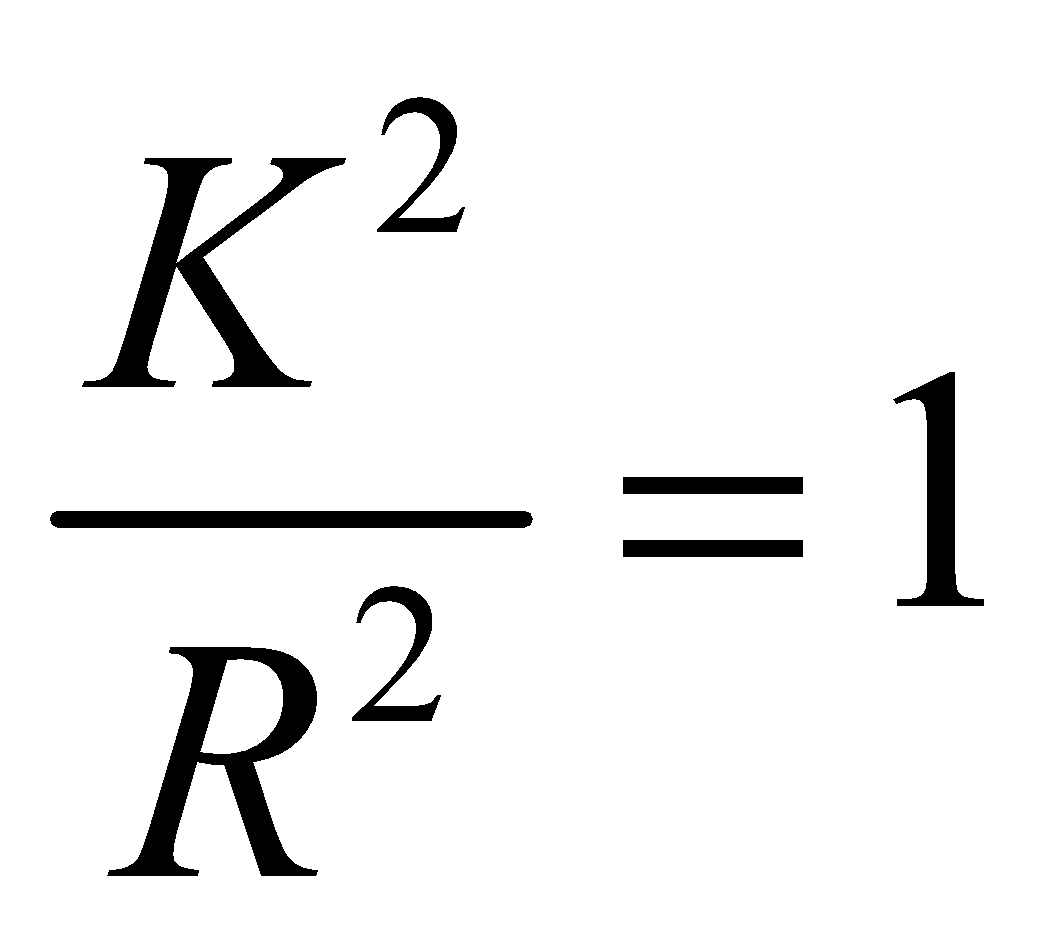
For disc 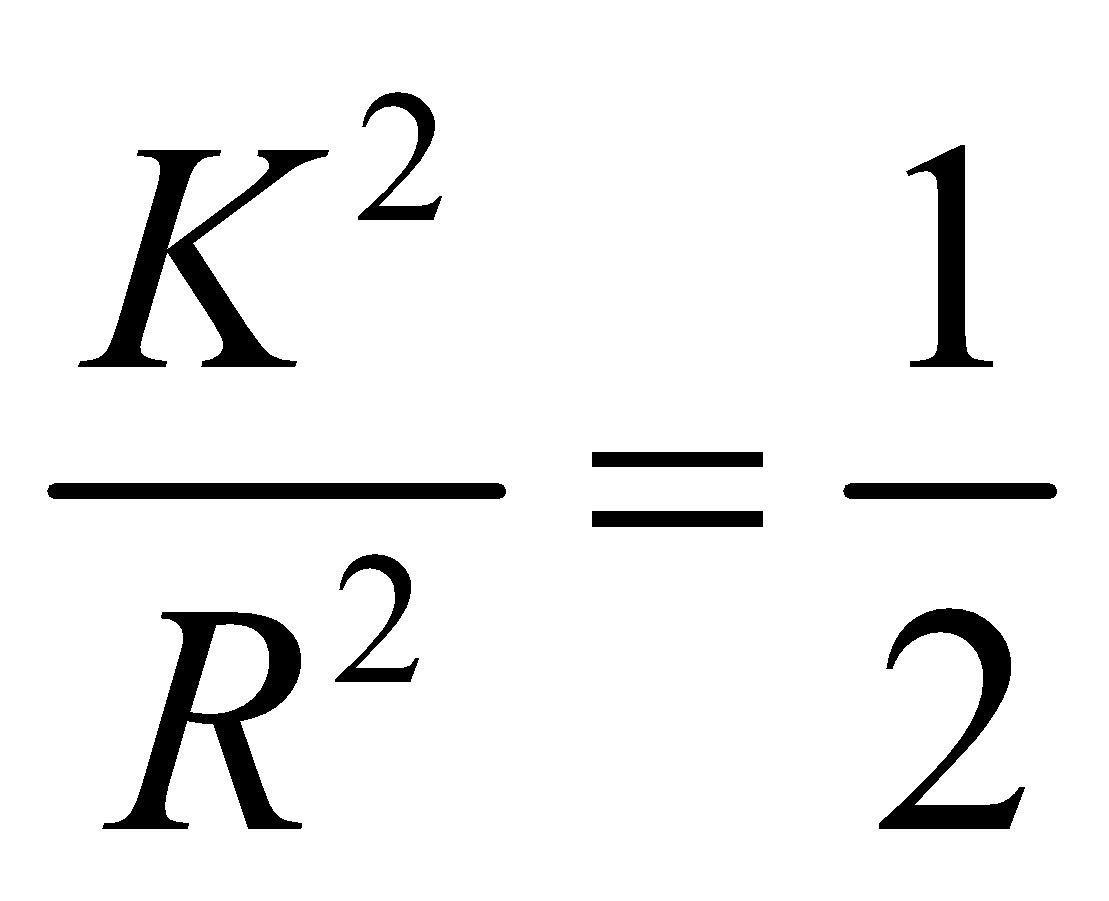
For sphere 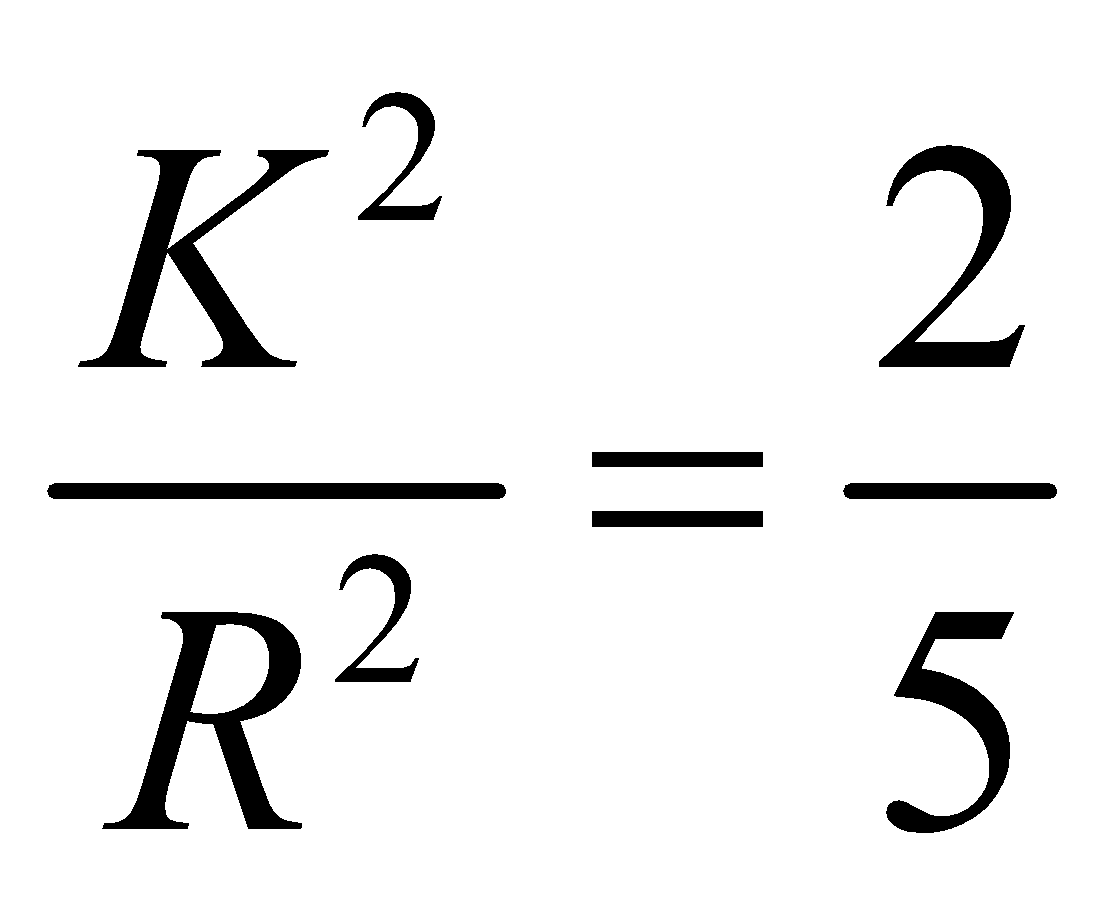
For shell 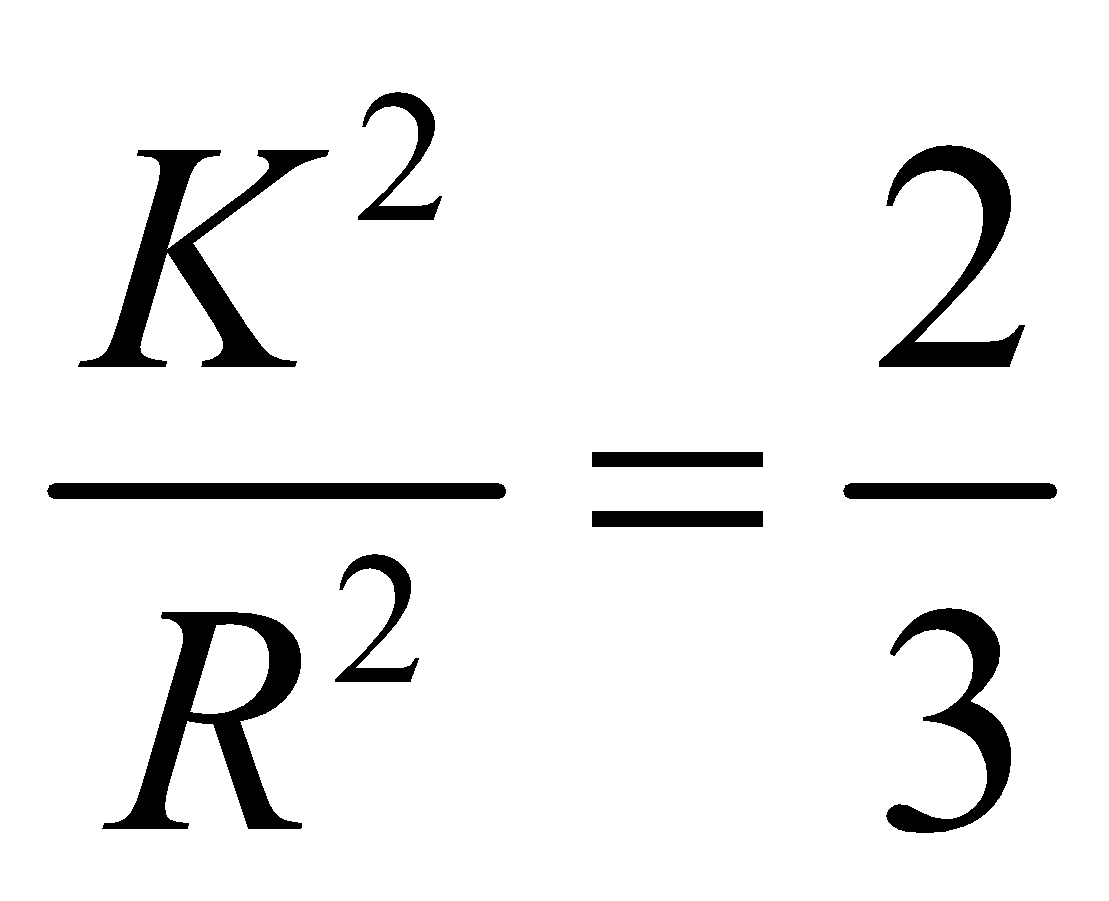
- The angular speed of all particles of a rotating/revolving rigid body is same, although their linear velocities may be different.
- Two particles moving with angular speed ω1 and ω2 on the same circular path and both in anti-clockwise direction then their relative angular speed will be ωr = ω1 – ω2.
In the above case one particle will complete one revolution more or less as compared to the other in time
- Let two particles move on concentric circles having radius r1 and r2 and their linear speeds v1, v2 both along anti-clockwise direction then their relative angular speed will be
- As I ∝ K2 and I = MK2, hence graph between I and K will be a parabola. However graph between log I and log K will be straight line.
- Rotational KE,
∴ Er ∝ ω2
∴ graph between 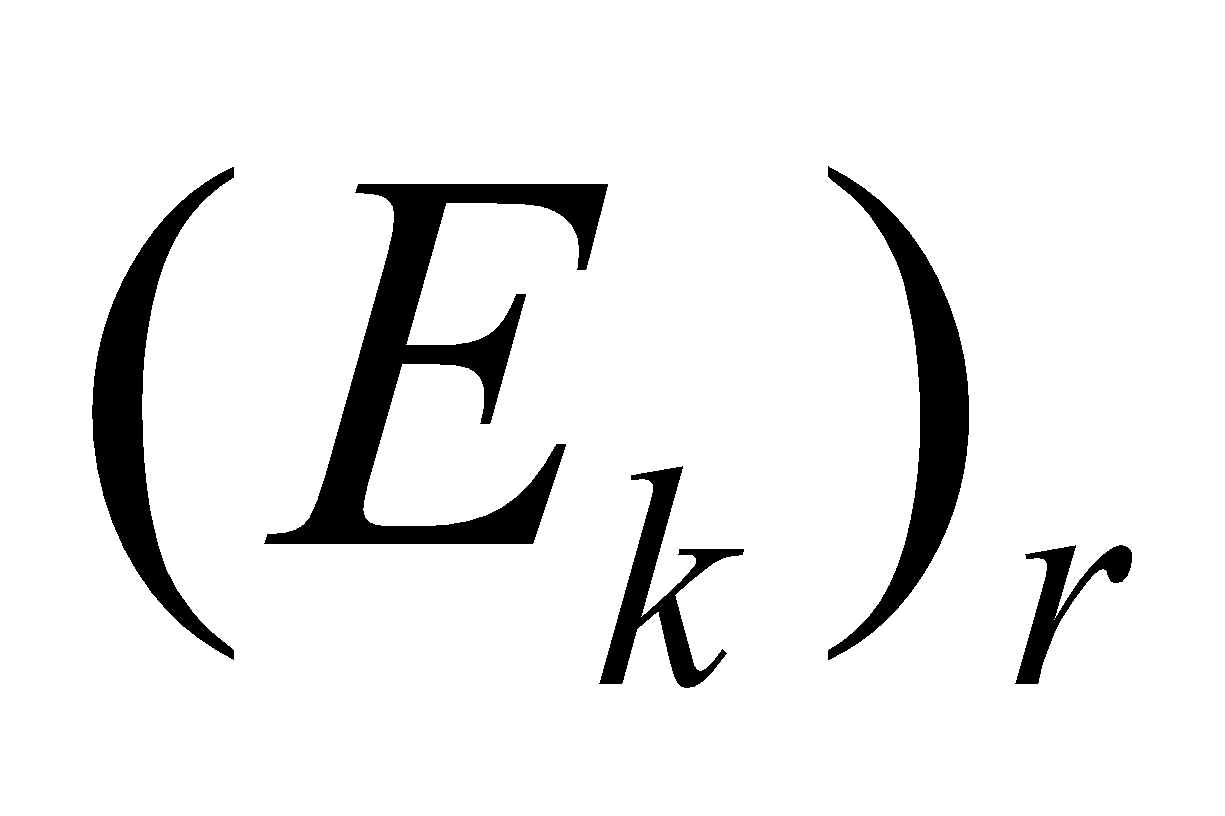 and ω will be as below
and ω will be as below
- Angular momentum L = Iω, hence L ∝ ω.
∴ Graph between L and ω is a straight line.
- The moment of inertia is not a vector quantity because clockwise or anti-clockwise, direction is not associated with it. It is a tensor.
- When a spherical/circular/cylindrical body is given a push, it only slips when the friction is absent, It may roll with slipping if friction is less than a particular value and it may roll without slipping if the friction is sufficient. (i.e.)
- When a body rolls without slipping no work is done against friction.



 9868233590
9868233590
